
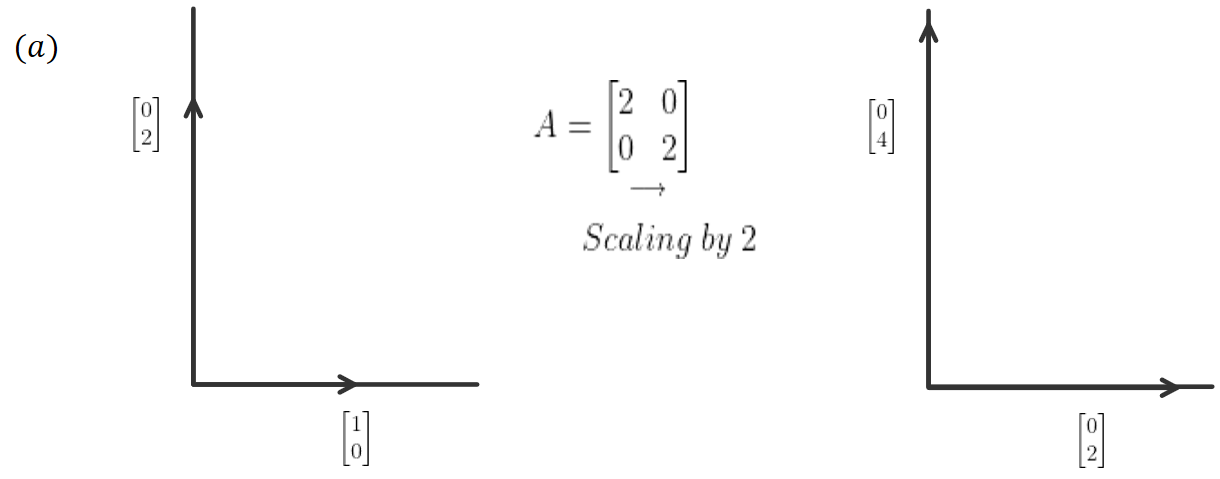
 ???
???
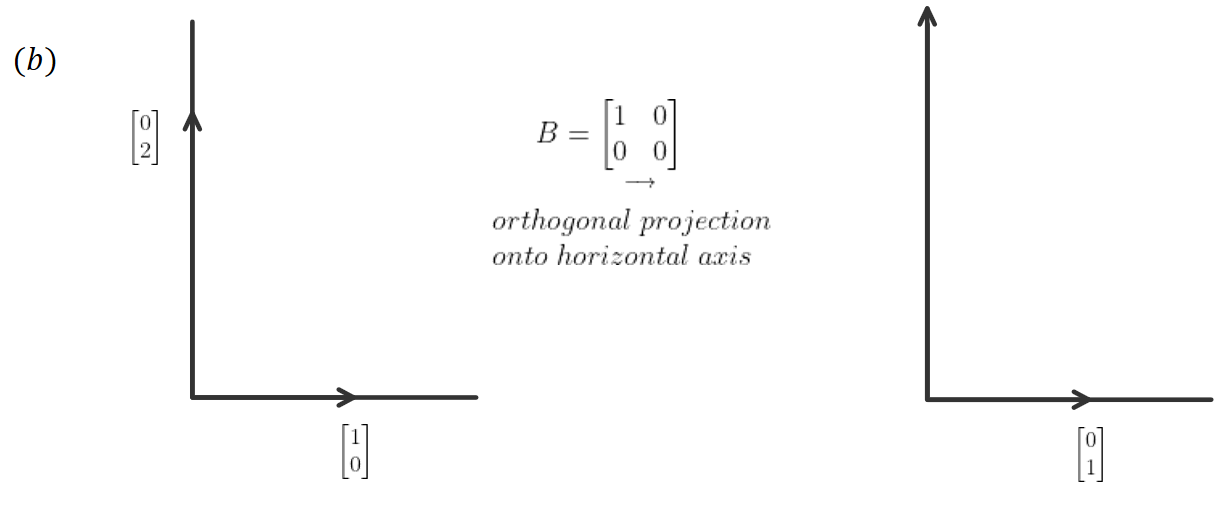
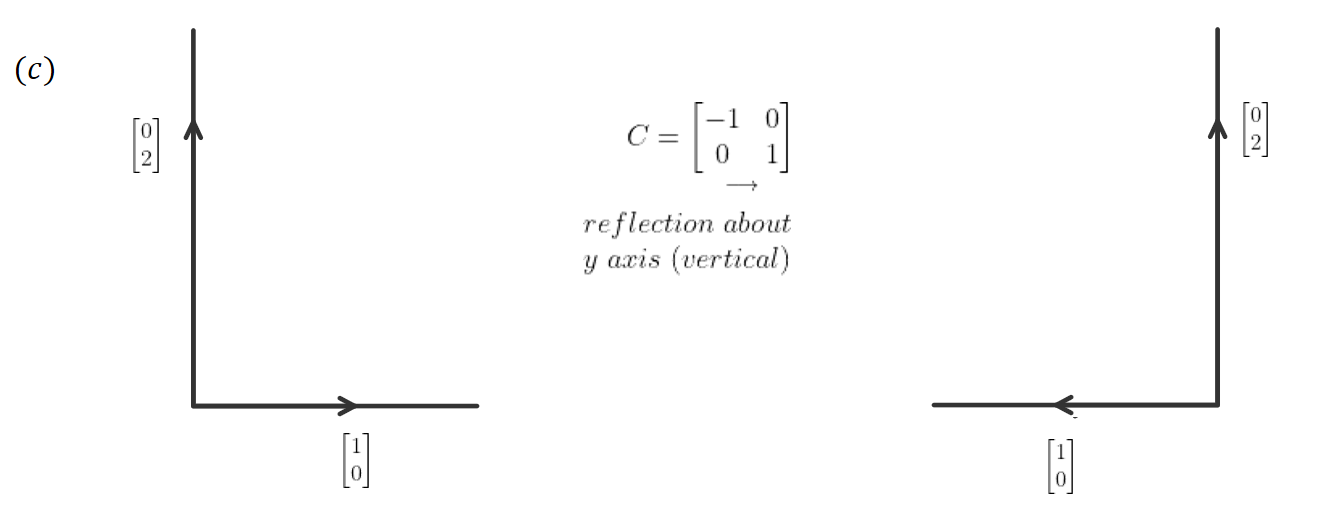
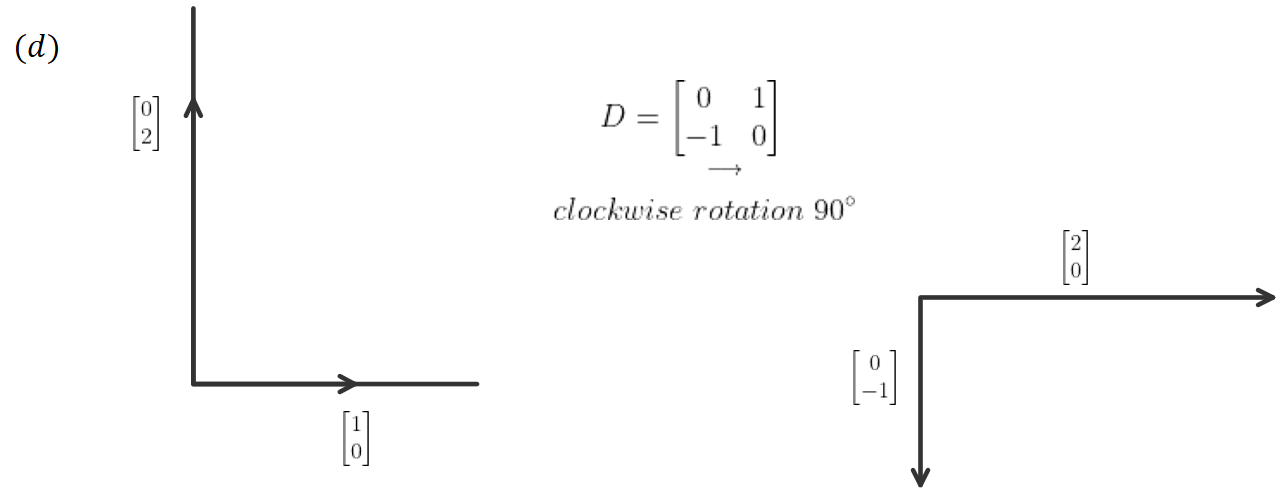

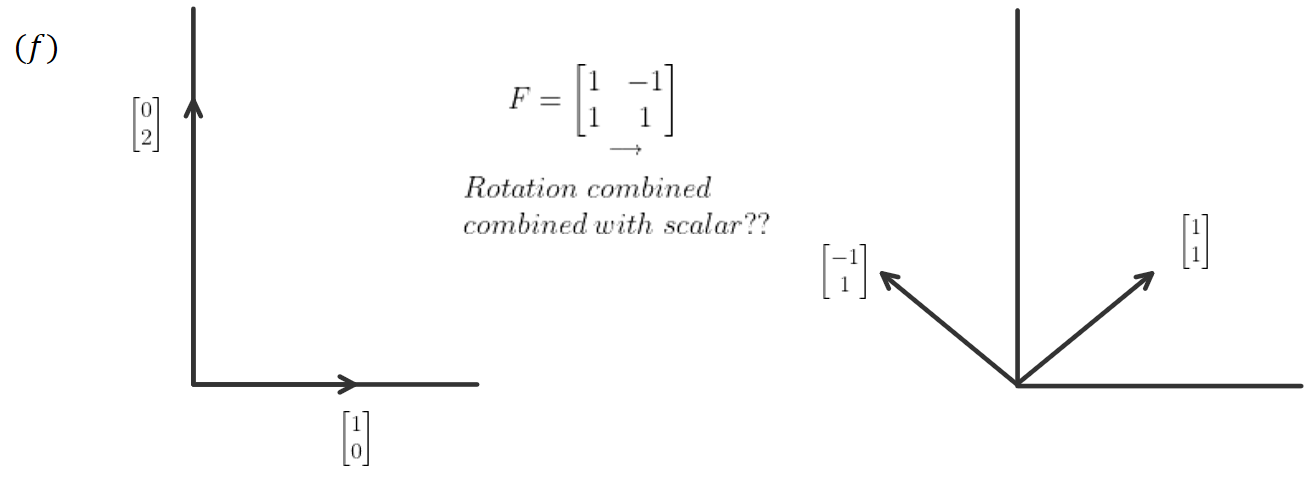
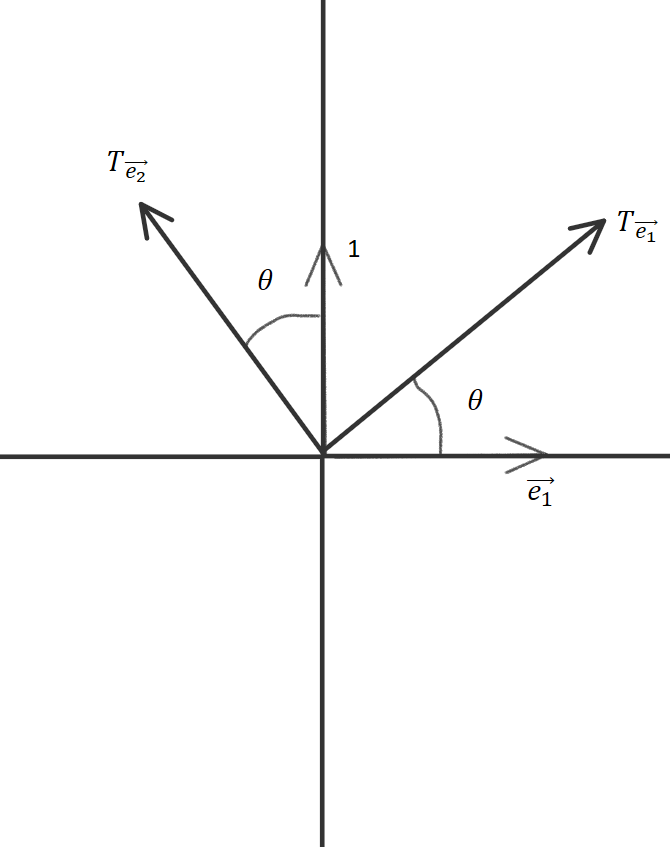
Vector Visualization
Vector Visualization
Vector Visualization Vector Visualization